Question

Use a quadratic equation to find two real numbers with a sum of -43 and a product of 306.

Answer 1

Real numbers = 39 and 9

Explanation:

The standard form of a quadratic equation is ax² + bx + c = 0

Given the following data;

a = 1

b = -43

c = 306

Quadratic equation formula is;

`x = \frac {-b \; \pm \sqrt {b^(2) - 4ac}}{2a}`

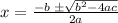
Substituting into the equation, we have;

`x = \frac {-(-43) \; \pm \sqrt {43^(2) - 4*1*306}}{2*1}`

`x = \frac {43 \pm \sqrt {1849 - 1224}}{2}`

`x = \frac {43 \pm \sqrt {625}}{2}`

`x = \frac {43 \pm 25}{2}`

`x_(1) = \frac {43 + 25}{2}`

`x_(1) = \frac {68}{2}`

`x_(1) = 39`

`x_(2) = \frac {43 - 25}{2}`

`x_(2) = \frac {18}{2}`

`x_(2) = 9`

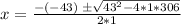
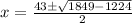
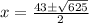
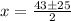
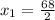
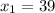
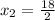
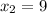
Therefore, the two real numbers are 39 and 9.

The quadratic equation now becomes;

x² - 43x + 306 = (x - 39)(x - 9) = 0