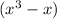We have been given the dimensions of the rectangular prism.
Lets say that the length, width, and height of the rectangular prism are:
Length

Width

Height
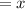
Volume of a rectangular prism is given by:
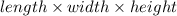
Plugging the values of length, width, and height, we get:
Total volume of the prism

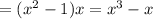 (we have used
(we have used
 )
)
So, the expression for the total volume of the prism is: