Question

He product of two positive numbers is 750. The first number is 5 less than the second number. The equation x(x – 5) = 750 can be used to find x, the value of the greater number. What is the value of the greater number? 15 25 30 50

Answer 1

30

Explanation:

You can try the answer choices to see what works.

15·10 ≠ 750

25·20 ≠ 750

30·25 = 750 . . . . the larger number is 30

50·45 ≠ 750

Answer 2

He product of two positive numbers is 750. The first number is 5 less than the second number. The equation x(x – 5) = 750 can be used to find x, the value of the greater number. What is the value of the greater number?

Solution

Here the second number is "x"

The first number is "x - 5"

The equation is x (x - 5) = 750

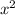`x^(2)`- 5x = 750

Subtract 750 from both sides, we get

`x^(2) -5x -750 =0\\`

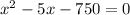
Solving the above quadratic equation using quadratic formula, we get

`x = \frac{-b+/- \sqrt{b^(2)-4ac } }{2a}`

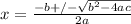
Here we have to plug in a =1, b = -5 and c = -750 in the above formula, we get

`x = (5 +/-√(3025) )/(2)`

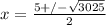
When we simplify the above expression is...

x = 30 and x = -25

x = -25 cannot be the solution since it is negative value.

x = 30 is the solution.

Here "x" represents the second number which is 30, that is the greater number.

Therefore, the answer is 30.