Question

Parallelogram ESTA has vertices E (10, 0), S (14, 3), T (6, 9), and A (2, 6). To calculate its area, Jamal will first determine the equation of the line through point E and perpendicular to ST. What is the equation of this line in point intercept form?

Answer 1

The vertices of parallelogram ESTA are E (10, 0), S (14, 3), T (6, 9), and A (2, 6).

As we know ,Area of parallelogram = Base × Height

As base can be determined by using distance formula because coordinates of the vertices are given.

Now to determine perpendicular, we will find the equation of line through E and perpendicular to ST.

Equation of line through S(14,3) and T(6,9) is

`(y-3)/(x-14)=(9-3)/(6-14)\\(y-3)/(x-14) =(6)/(-8)`

`(y-3)/(x-14)=(-3)/(4)\\4y -12=-3x+42`

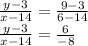
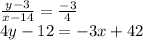
⇒4y + 3x =12+42

⇒ 3 x + 4 y=54

Equation of line perpendicular to ST and passing through E(10,0) is

4 x-3 y + k=0

Put x=10, y=0 in above equation is

4×10 -3×0 +k=0

⇒ k= -40

The Equation of line through point E and perpendicular to ST is

4 x-3 y -40=0