First, you must distribute 2(3x-1).
To do that, you will multiply 2•3x, and 2•-1 because you are taking the number outside of the parentheses and multiplying (distributing) it to all the numbers inside
After distributing, the left side of your inequality will be 6x-2
Now you have
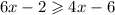
To find the value of x, you must subtract an x value from both sides of the equation, as well as a constant from each side.
so you have
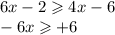
And that will make the equation
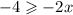
Now, divide the variable side, ***BUT, because you are dividing by a negative number in an inequality, the inequality will switch sides.
Then, the value of x is greater than or equal to 2