Question

carlos estimates that he will need to earn at least $700 to take his girlfriend to the prom. carlos works two jobs as show in the table jobs main st. Deli $8 per hour and babysitting $6 per hour. A. write an inequality to represent this situation B. Graph the inequality. C. will he make enough money if he works 50 hours at each job?

Answer 1

for the deli job he will make 400 and for the other job he makes 300. so he has just enough

Answer 2

The required inequality is:
`8x+6y\geq 700`

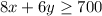
The required graph is shown in figure 1.

Yes, he make enough money.

Explanation:

Consider the provided information.

Part (A)

Carlos estimates that he will need to earn at least $700 to take his girlfriend to the prom.

Let the number of hours worked in Deli is x and the number of hours worked for babysitting is y.

Deli $8 per hour and babysitting $6 per hour. Carlos need to earn at least 700.

For at least use the inequity ≥

The required inequality is:
`8x+6y\geq 700`

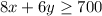
Part (B)

Rewrite the inequity as an equation to find the the x and y intercept.

`8x+6y=700`

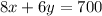
Substitute x=0 in the above

`8(0)+6y=700`

`y=(700)/(6)`

`y= 116.67`

Substitute y=0 in the above

`8x+6(0)=700`

`x =(700)/(8)`

`x= 87.5`

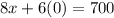
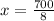
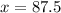
Use the point (0,116.67) and (87.5,0) to draw the graph.

Since the sign of inequality is greater than equal to, so shade the graph above the line. Use solid line as the sign of inequality is ≥.

Thus, the required graph is shown in figure 1.

Part (C)

We need to find he make enough money if he works 50 hours at each job.

Substitute x=50 and y=50 in the inequality.

`8(50)+6(50)\geq 700`

`400+300\geq 700`

`700\geq 700`

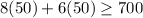
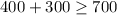
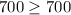
Which is true.

Hence, he make enough money.