Question

At a distance of 0.75 meters from its center, a Van der Graff generator interacts as if it were a point charge, with that charge concentrated at its center. A test charge at that distance experiences an electric field of 4.5 × 105 newtons/coulomb. What is the magnitude of charge on this Van der Graff generator?

Answer 1

Answer is 2.8 × 10-7 coulombs.

Answer 2

Since the Van de Graaff generator is given to behave like a point charge, we can use the equation for Electric Field, given as

`E = (kQ)/(r^(2) )`

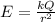
where,
`k = (1)/(4\pi ε₀)` =
`8.99 X 10^(9) (Nm^(2) )/(C^(2) )`

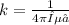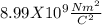
r is the distance between the generator and the test charge = 0.75 m

E is the magnitude of the Electric Field Strength =
`4.5 X 10^(5) N/C`

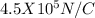
Rearranging the equation, making Q the subject of the formula, we have

`Q = (E.r^(2) )/(k)`

Plugging in the numerical values and simplifying them gets us

`Q = 0.2815 X 10^(-4) \\`

Thus, the charge on the Van de Graaff generator is 28.16 μC.