Since the Van de Graaff generator is given to behave like a point charge, we can use the equation for Electric Field, given as
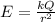
where,
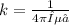 =
=
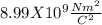
r is the distance between the generator and the test charge = 0.75 m
E is the magnitude of the Electric Field Strength =
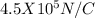
Rearranging the equation, making Q the subject of the formula, we have
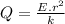
Plugging in the numerical values and simplifying them gets us
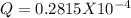
Thus, the charge on the Van de Graaff generator is 28.16 μC.