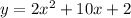Given points (5,102) (4,74) and (-2,-10)
We frame 3 equations using the given points
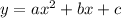
Plug in (5,102)
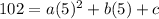
102 = 25a +5b + c -------> first equation
Plug in (4,74)
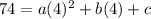
74 = 16a +4b + c----> second equation
Plug in (-2,-10)
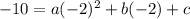
-10 = 4a -2b + c -----> third equation
Now we use the three equation and solve for a,b,c
Use first and second equation and subtract it
102 = 25a +5b + c
-74 = -16a -4b - c
----------------------------------
28 = 9a + b --------------> fourth equation
Subtract third equation from first equation
102 = 25a +5b + c
10 = -4a +2b - c
----------------------------------
112 = 21a + 7b --------------> fifth equation
Use fourth and fifth equation
28 = 9a + b
112 = 21a + 7b
Multiply the fourth equation by -7
-196= -63a -7b
112 = 21a + 7b
-----------------------
-84 = -42a
Divide by -42 on both sides
a= 2
Plug in the value of a=2 in fourth equation
28 = 9a + b
28 = 9(2) + b
28 = 18 + b ( subtract 18 from both sides)
b = 10
Plug in the values in third equation and find out c
-10 = 4a -2b + c
-10= 4(2) -2(10)+c
-10 = -12 + c
c= 2
We got a=2, b=10 and c=2
So equation becomes