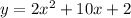Question

Please help! I just need the answer and I think a graphing calculator is needed for this

Answer 1

Given points (5,102) (4,74) and (-2,-10)

We frame 3 equations using the given points

`y=ax^2+bx+c`

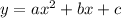
Plug in (5,102)

`102=a(5)^2+b(5)+c`

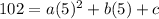
102 = 25a +5b + c -------> first equation

Plug in (4,74)

`74=a(4)^2+b(4)+c`

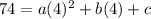
74 = 16a +4b + c----> second equation

Plug in (-2,-10)

`-10=a(-2)^2+b(-2)+c`

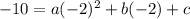
-10 = 4a -2b + c -----> third equation

Now we use the three equation and solve for a,b,c

Use first and second equation and subtract it

102 = 25a +5b + c

-74 = -16a -4b - c

----------------------------------

28 = 9a + b --------------> fourth equation

Subtract third equation from first equation

102 = 25a +5b + c

10 = -4a +2b - c

----------------------------------

112 = 21a + 7b --------------> fifth equation

Use fourth and fifth equation

28 = 9a + b

112 = 21a + 7b

Multiply the fourth equation by -7

-196= -63a -7b

112 = 21a + 7b

-----------------------

-84 = -42a

Divide by -42 on both sides

a= 2

Plug in the value of a=2 in fourth equation

28 = 9a + b

28 = 9(2) + b

28 = 18 + b ( subtract 18 from both sides)

b = 10

Plug in the values in third equation and find out c

-10 = 4a -2b + c

-10= 4(2) -2(10)+c

-10 = -12 + c

c= 2

We got a=2, b=10 and c=2

So equation becomes
`y=2x^2+10x+2`