Answer "and" Explanation:
You know that
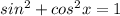 , so with the given information, you can write
, so with the given information, you can write
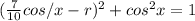
that becomes
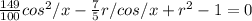
or as well

The condition for this equation to have real roots is
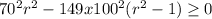
hence
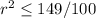
The roots of the quadratic equation
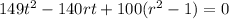 are in the interval [- 1, 1], because with the limitation
are in the interval [- 1, 1], because with the limitation
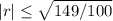 , the point of a minimum of the polynomial lies between - 1 and 1. Moreover, the polynomial evaluated at - 1 and 1 is > 0 for every r.
, the point of a minimum of the polynomial lies between - 1 and 1. Moreover, the polynomial evaluated at - 1 and 1 is > 0 for every r.
Solve for cos x and find the value of sin x.