Question

Solve 0.7cos(x)-sin(x)=r for x

where r is a real number

show all steps (if you don't show steps, I'll report the answer)

Answer 1

Answer "and" Explanation:

You know that
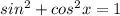`sin^(2) + cos^(2) x = 1`, so with the given information, you can write

`((7)/(10) cos/x-r)^(2) + cos^(2) x= 1`

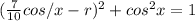
that becomes

`(149)/(100) cos^(2) / x- (7)/(5) r / cos /x + r^(2) - 1 = 0`

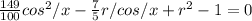
or as well

`149cos^(2) / x -140r / cos / x + 100(r^(2) - 1) = 0`

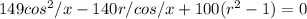
The condition for this equation to have real roots is

`70^(2) r^(2) - 149 x 100^(2) (r^(2) - 1) \geq 0`

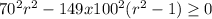
hence
`r^(2) \leq 149/ 100`

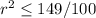
The roots of the quadratic equation
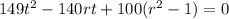`149t^(2) - 140rt + 100(r^(2) - 1) = 0` are in the interval [- 1, 1], because with the limitation
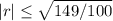`|r| \leq √(149/100)`, the point of a minimum of the polynomial lies between - 1 and 1. Moreover, the polynomial evaluated at - 1 and 1 is > 0 for every r.

Solve for cos x and find the value of sin x.

Answer 2

Try this solution (see the attachment), note:

1. the word 'ctgx' means 'cotangens x'; 2. this equation has roots not for all the real number 'r', it is shown in the 2-d line of the answer; 3. the answer is marked with red colour.