Question

Hey you guys plz help me with those 3 questions I will really appreciate your help. please. I will give 20+ pts.!!!

1. The California Tiger Salamander is an endangered species, which decreases at the rate of 4.6% per year in a habitat that currently has 60 of them. Write an exponential function and find how many California Tiger Salamanders will be left after 4 years.

2. Factor and solve the following equation 2x2 + x - 21 = 0.

3. Alvin throws the football to a receiver who jumps up to catch the ball. The height of the ball over time can be represented by the quadratic equation -4.9t2 + 7.5t + 1.8 = 2.1 . This equation is based on the acceleration of gravity -4.9 m/s2, the velocity of his pass is 7.5 m/s and releases the football at a height of 1.8 meters, and the height where the receiver catches the ball of 2.1 meters. Put the equation in standard form and then solve by using the quadratic equation.

Answer 1

Answer(1):

Decay formula is given by

`A=P(1-r)^t`

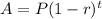
where P= present value = 60

r= percent rate of decay =4.6%=0.046

t= number of years

Plug these values into above formula to get required exponential function.

`A=60(1-0.046)^t`

`A=60(0.954)^t`

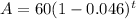
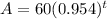
To find about how many California Tiger Salamanders will be left after 4 years, plug t=4

`A=60(0.954)^4=49.6986680074`

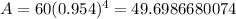
Hence final answer is approx 50 California Tiger Salamanders .

-----------

Answer(2):

`2x^2+x-21=0`

`2x^2-6x+7x-21=0`

`2x(x-3)+7(x-3)=0`

`(2x+7)(x-3)=0`

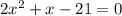
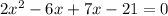
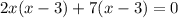
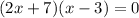
(2x+7)=0 or (x-3)=0

2x=-7 or x=3

x=-3.5 or x=3

Hence final answer is x=-3.5 , x=3.

-----------

Answer(3):

`-4.9t^2+7.5t+1.8=2.1`

`-4.9t^2+7.5t+1.8-2.1=0`

`-4.9t^2+7.5t-0.3=0`

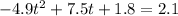
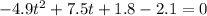
Hence standard form is
`-4.9t^2+7.5t-0.3=0`

where a=-4.9, b=7.5, c=-0.3

Plug that into quadratic formula

`t=(-b \pm √(b^2-4ac))/(2a)`

`t=(-7.5 \pm √((7.5)^2-4(-4.9)(-0.3)))/(2(-4.9))`

`t=(-7.5 \pm √(50.37))/(-9.8)`

`t=(-7.5 \pm 7.0972)/(-9.8)`

`t=(-7.5+7.0972)/(-9.8), \quad t=(-7.5-7.0972)/(-9.8)`

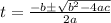
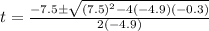
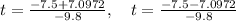
t=0.041, t=1.49

Hence final answer is t=0.041, t=1.49