Question

Need help as soon as possible!

What is the value of g(3)?

2
3
9
14

Answer 1

B) 3

Explanation:

Answer 2

g(x) is a piecewise function in such a way that it changes how it's defined based on what x happens to be. There are three cases

Case A: g(x) = x-1 but only if
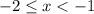`-2 \le x < -1` (x is between -2 and -1; including -2 but excluding -1)

Case B: g(x) = 2x+3 but only when
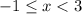`-1 \le x < 3` (x is between -1 and 3; including -1 but excluding 3)

Case C: g(x) = 6-x but only when
`x \ge 3`

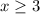
The input is x = 3 since we want to find the value of g(3). So we look at the 3 cases above (A,B,C) and determine that we use case C. Why? Because x = 3 makes
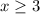`x \ge 3` true. Put another way, x = 3 is in the interval [3, infinty). So we'll use g(x) = 6-x to find that...

g(x) = 6-x

g(3) = 6-3

g(3) = 3

Answer: 3