Question

25 Points! (Linear Equations and Slope)

How do I solve for b in y=mx+b with only coordinates?
Please provide a good explanation, along with an answer and another explanation for the example!

Here's the example: (I've changed numbers from the original question)

What is the slope-intercept form of the equation of the line that contains the points (4, 2) and (8, -3) ?

Answer 1

You have to do change in y over change in x. So (2- -3) over (4 - 8) and you get 5/-4 or -1.25.

Then you take that and plug it in for m in y = mx + b. It would be y = -1.25x + b. Then you pick a coordinate that is given. (4,2) And plug it into the equation for x and y. That would change it to 2 = -1.25(4) + b. Then solve for b!

b = 7

or

y = -1.25x + 7.

Answer 2

You could do point-slope, but if you want to do it in slope-intercept:

y = mx + b

Using your example, we can start by finding the slope, which is
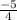`(-5)/(4)`. Plug in this slope and one of the points into the slope-intercept equation:

2 =
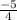`(-5)/(4)`(4) + b

Multiplying the slope, which has a denominator of 4, by 4 will just cancel out the denominator, giving you -5:

2 = -5 + b

Finish by adding 5 to both sides:

7 = b

Therefore, b = 7.

Hope this helps! :)