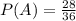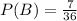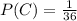Answer: The probabilities of winning a contract are
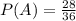
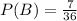
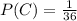
Let the Probability of C winning the contract - P(C) be 'X'
Then,
Probability of B winning the contract - P(B) will be '7X' and
Probability of A winning the contract - P(A) will be
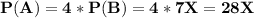
Since the total of all the probabilities is 1,
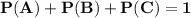
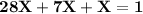
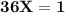
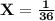
So,