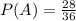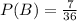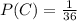Question

Three contractors (call them a, b, and

c.bid on a project to build an addition to the uva rotunda. suppose that you believe that contractor a is 4 times more likely to win than contractor b, who in turn is 7 times more likely to win than contractor

c. what are each of their probabilities of winning?

Answer 1

Answer: The probabilities of winning a contract are

`P(A) = (28)/(36)`

`P(B) = (7)/(36)`

`P(C) = (1)/(36)`

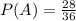
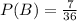
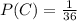
Let the Probability of C winning the contract - P(C) be 'X'

Then,

Probability of B winning the contract - P(B) will be '7X' and

Probability of A winning the contract - P(A) will be
`\mathbf{P(A) = 4 * P(B) = 4*7X = 28X}`

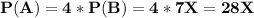
Since the total of all the probabilities is 1,

`\mathbf{P(A) + P(B) + P(C) =1}`

`\mathbf{28X + 7X + X =1}`

`\mathbf{36X =1}`

`\mathbf{X =(1)/(36)}`

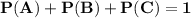
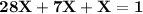
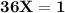
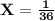
So,

`P(A) = (28)/(36)`

`P(B) = (7)/(36)`

`P(C) = (1)/(36)`