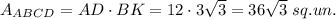Question

Given: ABCD ∥gram, BK ⊥ AD , AB ⊥ BD AB=6, AK=3 Find: m∠A, BK, Area of ABCD

Answer 1

1. Consider right triangle ABK. In this triangle AB is the hypotenuse, BK and AK are legs. By the Pythagorean theorem,

`AB^2=AK^2+BK^2,\\\\6^2=3^2+BK^2,\\\\BK^2=36-9=27,\\\\BK=3√(3)\ un.`

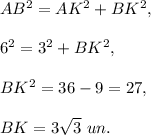
2. Use the definition of
`\cos \angle A:`

`\cos \angle A=\frac{\text{adjacent leg}}{\text{hypotenuse}}=(AK)/(AB)=(3)/(6)=(1)/(2).`

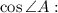
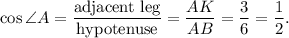
Then
`m\angle A=60^(\circ).`

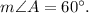
3. Consider right triangle ABD. In this triangle AD is the hypotenuse, AB and BD are legs. Since
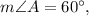`m\angle A=60^(\circ),` then

`m\angle BDA=180^(\circ)-90^(\circ)-60^(\circ)=30^(\circ).`

The leg that is opposite to the angle of 30° is half of the hypotenuse, so

`AD=2AB=12\ un.`

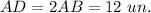
4. The area of parallelogram aBCD is

`A_(ABCD)=AD\cdot BK=12\cdot 3√(3)=36√(3)\ sq. un.`