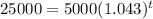The correct option is: B.
Step-by-step explanation
The general form of growth equation is:
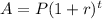 , where A = final amount, P = initial amount, r = growth rate in decimal form and t = time duration
, where A = final amount, P = initial amount, r = growth rate in decimal form and t = time duration
Here, the speed of the rocket at the beginning was 5,000 kilometers per hour and at the end will be 25,000 kilometers per hour. The speed increases at a rate of 4.3% per minute.
That means,
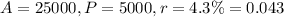
Now plugging these values into the above equation, we will get......
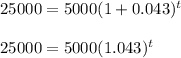
So, the equation that could be used to determine the time for the speed of the rocket to reach 25,000 kilometers per hour will be: