We know from the question that the Mass of the elastic object m = 0.00040 kg
Its Spring Constant is given as k = 40.0 N/m
Velocity required when the object is launched V = 16.0 m/s
Distance the elastic object has to be stretched from the equilibrium x = ?
We can use Conservation of Energy in this case, which tells us that
Elastic Potential Energy stored in the elastic object = Kinetic energy gained by it when released
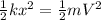
We see that the 1/2 cancels from both sides and we are left with
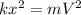
Making x the subject of the formula, we have
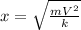
Plugging in the numbers and solving for x, we get
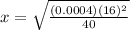
Therefore, x = 0.05 m
The object has to be stretched by 0.05 m from its equilibrium position.