Question

a ship travels a port p and travels 30 km due north. then it changes course and travels 20 km in a direction  30° east of north to reach port r. calculate the distance from P to R.

Answer 1

When we represent what is given to us on a coordinate plane, we have a figure as shown in the attachment.

To find the distance between P and R, we have to find the Net Displacement of the ship (brown arrow in the figure).

For that, we use the rules for Vector addition.

We see that the first displacement
`D_(1)` = 30 km (blue arrow) is along the y-axis, but the second part of the ship's journey
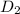`D_(2)` = 20 km (red arrow) is at an angle with reference to y-axis.

So, we first find the components of the red arrow along X and Y.

Component of
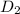`D_(2)` along X-axis is given by
`D_(2x)  = D_(2) Sin 30` = 10 km

Component of
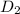`D_(2)` along Y-axis is given by
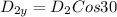`D_(2y)  = D_(2) Cos 30` = 17.32 km

We now add all the vectors along X and along Y separately.

Net Displacement along X
`D_(netX) = 10 km`

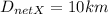
Net Displacement along Y
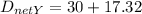`D_(netY) = 30 + 17.32` = 47.32 km

Now that we have the components of the net displacement along X and Y, we make use of Pythagorean Theorem to calculate the
`D_(net)`

`D_(net)  = \sqrt{D_(netX) ^(2) + D_(netY) ^(2)}`

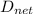
Therefore, [tex]D_{net} = 48.37 km.

Hence, the distance between the ports P and R is 48 km.