Question

A soccer player kicks a ball at an angle of 35 degrees above horizontal with velocity of 25 m/s. Assuming there is no air friction, what is the horizontal component of the ball's velocity 1 s after the ball left her foot?

A) 4.5 m/s

B) 14.3 m/s

C) 15.2 m/s

D) 20.5

Answer 1

The ball's horizontal velocity is constant throughout its trajectory, with a magnitude of

`v_(0x)=\left(25\,(\mathrm m)/(\mathrm s)\right)\cos35^\circ=20.5\,(\mathrm m)/(\mathrm s)`

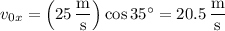
If the ball has landed before 1 second has passed, then its velocity will be zero, so we should check if that's the case before we wrap up. The ball's vertical position in the air is given by

`y=y_0+v_(0y)t-\frac g2t^2`

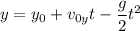
where we can assume
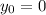`y_0=0` is the ball's initial position, and
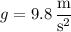`g=9.8\,(\mathrm m)/(\mathrm s^2)` is the acceleration due to gravity. Then the time it takes for the ball to reach the ground after being kicked is

`0=\left(25\,(\mathrm m)/(\mathrm s)\right)\sin35^\circ\,t-\frac g2t^2\implies t=0\text{ or }t=2.93\,\mathrm s`

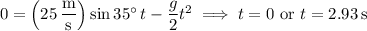
So it takes the ball 2.93 seconds to reach the ground, so that after 1 second in particular, the ball's horizontal velocity is still 20.5 m/s.