We have to solve the system of equations by Cramer's rule.
The coefficient matrix is given by

Let us find the determinant of coefficient matrix.

For X-matrix

Now, we find its determinant

For Y-matrix
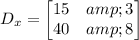
Now, we find its determinant
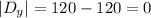
Therefore, the value for x is given by
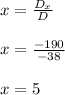
The value for x is 5.