Question

Using Cramer’s Rule, what is the value of x in the system of linear equations below?

3X+4Y=15
8X-2Y=40

Answer 1

D) x=5

Explanation:

Edge 2021 :)

Answer 2

We have to solve the system of equations by Cramer's rule.

The coefficient matrix is given by

`D=\begin{bmatrix}3&4\\8 &-2\end{bmatrix}`

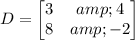
Let us find the determinant of coefficient matrix.

`|D|= -6-32=-38`

For X-matrix

`D_x=\begin{bmatrix}15&4\\40 & -2\end{bmatrix}`

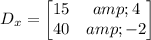
Now, we find its determinant

`|D_x|=-30-160=-190`

For Y-matrix

`D_x=\begin{bmatrix}15&3\\ 40&8\end{bmatrix}`

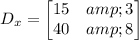
Now, we find its determinant

`|D_y|=120-120=0`

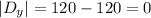
Therefore, the value for x is given by

`x=(D_x)/(D)\\\\x=(-190)/(-38)\\\\x=5`

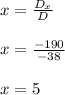
The value for x is 5.