Question

If 2x < 100 and x is an integer, how many of the 2x + 2 integers will be divisible by 3 and by 2?

(a) 1
(b) 2
(c) 3
(d) 4
(d) 5

Answer 1

the answer will be (d) 5 , I am not really sure

Answer 2

this is a great question!

several ways to solve this, but I'm going to use the straight forward approach

how many integers satisfy

`2x < 100`
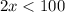
solve this

`2x < 100 \\ (2x)/(2) < (100)/(2) \\ x < 50`
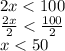
so we have less than 50 options to pick from. 49 to be exact.

out of those, we have the rule that when we multiply it by 2 then add, we can divide it by 2. this will always give us an even number, so dont worry with that. we need to focus on being divisible by 3.

so, let's look for a pattern.


`2(1) + 2 = 4 \: \: \: no \\ 2(2) + 2 = 6 \: \: \: yes \\ 2(3) + 2 = 8 \: \: \: no \\ 2(4) + 2 = 10 \: \: \: no \\ 2(5) + 2 = 12 \: \: \: yes \\ 2(6) + 2 = 14 \: \: \: no \\ 2(7) + 2 = 16 \: \: \: no \\ 2(8) + 2 = 18 \: \: \: yes`

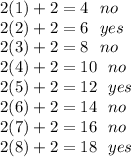
so, every 3rd 2x+2 integer is divisible by three

we are counting by 2s so there are 24 of them between 2 and 49. (48 is the biggest one less than 49 and 48/2 is 24)

if it is every 3, then we divide 24 by 3, giving me 8.

the list is 6,12,18,24,30,36,42,48

is there a part of this question you forgot to write?

just from a teacher's standpoint, you did not state whether the integers are positive, so the answer is really an unlimited amount