We are given an equation of line x - 2y = -6.
We need to find the area between the line and the two axes.
In order to find the area, we need to graph the triangle first.
Let us find x and y-intercepts of the graph to graph it on coordinates axes.
In order to find x-intercept, we need to plug y=0.
Plugging y=0 in given equation, we get
x-2(0) =-6.
x-0=-6.
x=-6.
So, x-intercept = -6.
In order to find y-intercept, we need to plug x=0.
Plugging x=0 in given equation, we get
0-2y=-6.
-2y=-6.
Dividing both sides by -2, we get
y=3.
So, y-intercept is =3.
Let us graph now.
We can see from the graph, base of the triangle = 6 units and height of the triangle=3 units.
We know formula for area of a triangle.
Area =
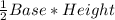
Plugging values of base =6 and height =3 in above formula, we get
Area =
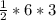
=

= 9 square units.
Therefore, area between the line x - 2y = -6 and the two axes is 9 square units.