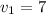
x = 4
y = 3
From the diagram, it is clear that the x and y are the component of the
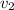 vector. Since, x and y are perpendicular.
vector. Since, x and y are perpendicular.
Hence,
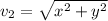
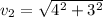
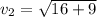
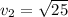
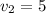
Now,
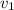 and x are in the same direction. Hence, we can add the magnitude.
and x are in the same direction. Hence, we can add the magnitude.
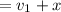
= 7 + 4
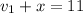
y and
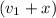 are perpendicular and they are the components of R
are perpendicular and they are the components of R
Hence, the magnitude of R:
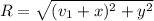
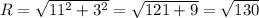
R = 11.4