We have to find the perimeter of the triangle KLM.
We have been given that the length of the side LM=12,
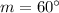 , and
, and
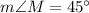
Refer the attached image.
In a triangle sum of three angles should be
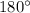 .
.
So,
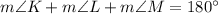
Plugging the values of angle K and angle M, we get:
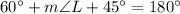
So,
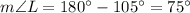
Now, that we have the measure of angle L, we will apply sine rule to find the length of the sides KL and KM.
Using the sine law for the triangle KLM, we get:

Refer the image. Plugging the value of the sides of the triangle KLM and the angles of the triangle KLM, we get:
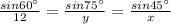
Now using,

We get the value of 'y'
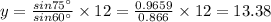
So the length of the side KM is 13.38 units.
Now using,
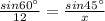
We get the value of 'x'
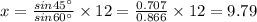
So the length of the side KL is 9.79 units.
Now, to find the perimeter of the triangle KLM we need to sum up the length of the sides of the triangle KLM.
The perimeter of the triangle KLM
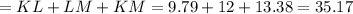 units
units