Question

Given a soda can with a volume of 36 and a diameter of 4, what is the volume of a cone that fits perfectly inside the soda can? (Hint: only enter numerals in the answer blank).

Numerical Answers Expected!

Answer 1

the volume of the cone is 12

Answer 2

Explanation:

We know

Volume of a cylinder is
`V = \pi r^(2)h`

`V = \pi \left ((D)/(2)\right )^(2)h`

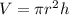
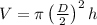
where V is volume of the soda can = 36 (given )

D is diameter = 4 (given )

h is the height of the soda can

`V = \pi \left ((D)/(2)\right )^(2)h`

`V = \pi (D^(2))/(4)h`

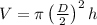
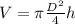
36 = 3.14 x (16/4) x h

36 = 3.14 x 4 x h

36 = 12.56 x h

∴ 36 / 12.56 = h

h = 2.87

Now we know that the volume of a cone is given by

`V = \pi*  (D^(2))/(4)* (h)/(3)`

`V = \pi*  (4^(2))/(4)* (2.87)/(3)`

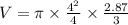
= 3.14 x 4 x 0.95

= 11.932

= 12 (approx.)

Therefore 12 units cube of volume can be easily fitted in a soda can of 36 unit cubes.