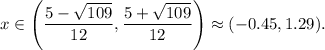Question

On what interval/s is the following function decreasing? (Use interval notation. Round answers to 2 decimal places.)

m(x) = 4x^3 - 5x^2 - 7x

please explain how you do it, thank you!

Answer 1

You are given the function
`m(x) = 4x^3 - 5x^2 - 7x.`

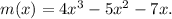
1. Find the derivative m'(x):

`m'(x)=4\cdot 3x^2-5\cdot 2x-7=12x^2-10x-7.`

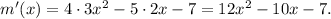
2. Find stationary points, solving the equation m'(x)=0:

`12x^2-10x-7=0,\\ \\D=(-10)^2-4\cdot 12\cdot (-7)=100+336=436,\\ \\√(D)=√(436)=2√(109),\\ \\x_1=(10-2√(109))/(24)=(5-√(109))/(12),\ x_2=(10+2√(109))/(24)=(5+√(109))/(12).`

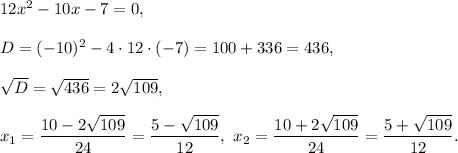
3. Determine the signs of derivative:

• when
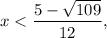  `x<(5-√(109))/(12),` then
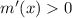  `m'(x)>0` (function is increasing);
• when
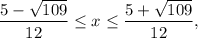  `(5-√(109))/(12)\le x\le (5+√(109))/(12),` then
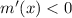  `m'(x)<0` (function is decreasing);
• when
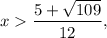  `x>(5+√(109))/(12),` then
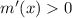  `m'(x)>0` (function is increasing).

Thus, function is decreasing for
`x\in \left((5-√(109))/(12), (5+√(109))/(12)\right)\approx (-0.45,1.29).`