Question

Given the function: f(x) = x2 – 2x How can you restrict the domain so that f(x) has an inverse? What is the equation of the inverse function? x ≥ 0; f Superscript negative 1 Baseline (x) = 1 + StartRoot x + 1 EndRoot x ≥ 1; f Superscript negative 1 Baseline (x) = 1 + StartRoot x + 1 EndRoot x ≥ 0; f Superscript negative 1 Baseline (x) = 1 minus StartRoot x + 1 EndRoot x ≥ 1; f Superscript negative 1 Baseline (x) = 1 minus StartRoot x + 1 EndRoot

Answer 1

D x > 2; f Superscript negative 1 Baseline (x) = 2 + StartRoot x + 2 EndRoot

Explanation:

Apply this method when doing problems similar to this one.

Answer 2

9514 1404 393

Answer:

(b) x ≥ 1; f⁻¹(x) = 1+√(x+1)

Explanation:

We can find the inverse function by solving for y:

x = f(y)

x = y² -2y

x +1 = y² -2y +1

x +1 = (y -1)²

√(x +1) = y -1

1 +√(x +1) = y

So, the inverse function is ...

`f^(-1)(x)=1+√(x+1)`

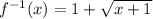
For this, the root will be non-negative, so the minimum value of this function is 1. That is, the minimum value of x for which the original function has this as an inverse is 1.

The domain restriction is x ≥ 1.

The inverse function is f⁻¹(x) = 1+√(x+1)