Answer:
 .
.
Explanation:
We have been given two functions as:
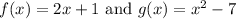 . We are asked to find
. We are asked to find
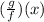 .
.
By the definition of composite function
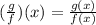 .
.
Upon substituting
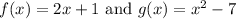 in our equation, we will get:
in our equation, we will get:

We cannot further simplify our given equation, therefore,
 would be our answer.
would be our answer.