Observe the figure.
After the given statements as:
Statement 1:
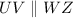
Statement 2: Points S,Q,R and T are all lie on the same plane.
Statement 3:
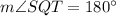
Statement 4:
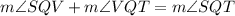
Statement 5:
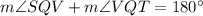
Now, the next statement is as:
Statement 6:
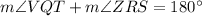 which is statement III.
which is statement III.
(Same side interior angles theorem)
Statement 7:
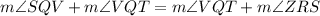 which is statement II.
which is statement II.
(Substitution property of equality)
Statement 8:
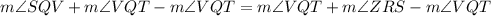
 which is statement I.
which is statement I.
(Subtraction property of equality)
So, the correct order of the given reasons to complete the proof is III, II, I.
Therefore, Option 4 is the correct answer.