Question

G(x) = 3x^2 – 14x – 5 

- State the y-intercept (state your answer as an ordered pair)

- State the x-intercept/s (state your answer/s as an ordered pair)

- State the maximum and/or minimum values (state your answer/s as an ordered pair)

- State the intervals that the function is increasing/decreasing.

- State the intervals that the function is positive/negative.

- State if the function has even, odd, or no symmetry.

- State the domain and range? (State your answers in inequality and interval notation)

Answer 1

G(x) = 3x² – 14x – 5

y-intercept is always at x = 0.

G(0) = 3(0)² -14(0) -5 = -5

So y-intercept is (0, -5).

x-intercept is always at y=0.

G(x) = 3x² – 14x – 5 = 0

3x² – 15x + x – 5 = 0

3x(x-5) + 1(x-5) = 0

(3x+1)(x-5) = 0

x = -1/3 or x = 5

So x-intercepts are (-1/3, 0) and (5, 0).

given is G(x) = 3x² – 14x – 5

Maximum or minimum occurs at vertex where x = -b/2a

`x = (-b)/(2a) =(-(-14))/(2(3)) =(14)/(6)= (7)/(3) =2.3`

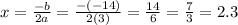
G(2.33) = 3(2.3)² -14(2.3) -5 = 3(5.4) -32.2 -5 = 16.2 -37.2 = -21.

Hence, minimum value is at (2.3, -21)

Function decrease from negative infinity to vertex i.e. (-infinity, 2.3)

Function increases from vertex to positive infinity i.e. (2.3, +infinity)

The function is negative in between the x-intercepts i.e. (-1/3, 5)

The function is positive outside the interval of x-intercepts i.e. (-infinity, -1/3) U (5, +infinity).

The function is even iff f(-x) = f(x), and it is odd iff f(-x) = -f(x).

Here G(-x) = 3x² +14x -5 is neither g(x) nor -g(x).

So, the function has no symmetry.

The domain of any quadratic function is Real numbers. The range of any quadratic function is y ≥ minimum value OR y ≤ maximum value.

So, Domain is -∞ ≤ x ≤ ∞ or (-infinity, +infinity)

Range is y ≥ -21 or (-21 , +infinity)