Question

Given: ABCD ∥gram, BK ⊥ AD , AB ⊥ BD AB=6, AK=3 Find: m∠A, BK, A

Answer 1

Given: ABCD ∥gram,

BK ⊥ AD , AB ⊥ BD

AB=6, AK=3

Find: m∠A, BK

To proof

as given BK ⊥ AD

thus ΔABK is a right triangle.

thus by using the pythagoras theorem

we have

AB² = BK² + AK²

BK² = AB ²- AK²

= 6² - 3²

= 36 - 9

= 27

Hence

BK =
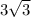`3√(3)` unit

Now find the value m∠A

by using the trignometric function

FORMULA

cosA =
`(BASE)/(HYPOTENUSE)`

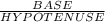
cosA =
`(3)/(6)`

=
`(1)/(2)`

m∠A = 60°

hence proved