Question

Does knowing the distance between two objects give you enough information to locate the objects? explain

Answer 1

By knowing the distance between two objects we can not get enough ideas about the location of these respective objects. It can be easily understood from a simple example.

Let us consider two bodies A and B which are in a two dimensional plane. .Let the co-ordinates of body A is [2,2].

Let us consider two possible co-ordinate pairs [1,0] and [0,1]

Let the body B is at [1,0].

Hence the distance between A and B is
`AB=√([2-1]^2+[2-0]^2)`

`AB=√(1+4)`

`AB=√(5)`

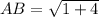
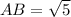
Let the body B is shifted to [0,1] now.

Now the distance between A and B will be
`AB=√([2-0]^2+[2-1]^2)`

`AB=√(4+1)`

`AB=√(5)`

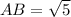
Here we observe that distance in each case is same .But in first case the body B was on +X- axis while in second case the body B was on +Y- axis.

Hence distance between points may be same in different planes, but only the distance can not get enough ideas about the location of the objects.It is the points in specific reference frames gives the ideas about the location of the objects. As position is relative ,hence for complete location of a object,the observer also plays a vital role here.