Question

The distribution coefficient, k , 10 for compound y. what weight of compound y would be removed from a solution of 4.0 g of y in 100 ml water by a single extraction with 100 ml of ether?

Answer 1

Answer : The weight of compound y would be removed is 3.6363 g.

Solution : Given,

Distribution coefficient, K = 10

Volume of ether (organic layer) = 100 ml

Volume of water (aqueous layer) = 100 ml

Total Weight of material dissolved = 4 g

Formula used :

`K=([Solute]_(o) )/([Solute]_(aq))=(C_(o) )/(C_(aq))=(W_(o)/V_(o)  )/(W_(aq)/V_(aq)  )`

Where,

'O' repersent for organic layer and 'aq' repersent for aqueous layer.

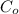`C_(o)` and
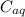`C_(aq)` are the concentration of organic solution and the concentration of aqueous solution respectively.

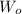`W_(o)` and
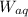`W_(aq)` are the weight of material dissolved in each organic and aqueous layer respectively.

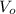`V_(o)` and
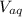`V_(aq)` are the volume of organic and aqueous layer respectively.

Let, the weight of compound y removed '
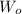`W_(o)`' is 'X' gram.

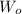`W_(o)` = X gram

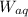`W_(aq)` = Total weight of material - weight of compound y removed = 4 - X gram

Now put all the values in above formula,we get

`K=(W_(o)/V_(o))/(W_(aq)/V_(aq))`

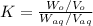
10=
`((X(g))/(100(ml)) )/((4-X(g))/(100(ml)) )`

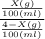
Rearranging the terms, we get the value of X, as

X = 3.6363 g