Answer:
Approximately
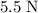 , assuming that the volume of these two charged objects is negligible.
, assuming that the volume of these two charged objects is negligible.
Step-by-step explanation:
Assume that the dimensions of these two charged objects is much smaller than the distance between them. Hence, Coulomb's Law would give a good estimate of the electrostatic force between these two objects regardless of their exact shapes.
Let
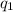 and
and
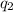 denote the magnitude of two point charges (where the volume of both charged object is negligible.) In this question,
denote the magnitude of two point charges (where the volume of both charged object is negligible.) In this question,
 and
and
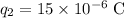 .
.
Let
 denote the distance between these two point charges. In this question,
denote the distance between these two point charges. In this question,
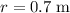 .
.
Let
 denote the Coulomb constant. In standard units,
denote the Coulomb constant. In standard units,
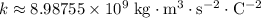 .
.
By Coulomb's Law, the magnitude of electrostatic force (electric force) between these two point charges would be:
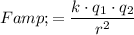 .
.
Substitute in the values and evaluate:
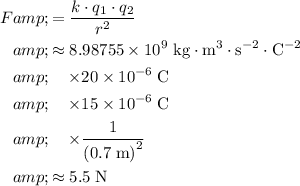 .
.