Question

• a helicopter hovering at 10 m above the ground is shining a spotlight at a person 30 m away1 . if the person is 2 m tall how long is the shadow she casts. • assume the person is running towards the helicopter at 2 m/s and the helicopter is descending at 1 m/s. what is the rate of change of the length of the shadow at the precise moment that the helicopter is 10 m above the ground and 30 m away from the person? problem 2. the volume of a sphere of radius r is v (r) = 4 3 πr3 .

a. compute the derivative of v (r) with respect to r,
b. the surface area of a sphere of radius r is 4πr2 . compare th

Answer 1

As shown in the figure

Height of helicopter above the ground=30 m

Distance from the base to the point where the person is standing=30 m

height of the person=2 m

Now the person cast the shadow of length x m.

Triangle ABC and triangle EDC are similar.

∵ ∠B= ∠D=90°

∠C is common.

So by AA similarity ΔABC and ΔEDC are similar.

As we know when triangles are similar their sides are proportional.

AB/AD =BC/DC

Let DC=x meter

⇒
`(10)/(x)=(30+x)/(x)`

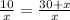
⇒5=\frac{30+x}{x}[/tex]

⇒5x=30+x

⇒4x = 30

⇒ x=30/4

⇒ x=7.5 meter

So length of shadow=7.5 meter

2. volume of a sphere of radius r is v (r) =
`(4)/(3)π r^(3)`

`\frac{\mathrm{d} }{\mathrm{d} r}V`=4/3π×3
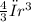
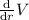`r^2`

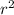
=4π
`r^2`

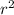
surface area of a sphere of radius r is 4π
`r^2`

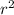
b) Ratio of derivative of volume of sphere to surface area of sphere=
`(4\pi r^2)/(4\pi r^2)`

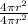
=1 [ incomplete question but you have written few words ]