orbital velocity of an object around earth is given by
here we can assume that object is moving at distance "r" from the center of earth
and net gravitational force on the object will provide it centripetal force to revolve in the circle
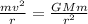
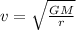
so here we have
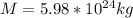
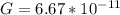
now if the object is projected from surface of earth
then we have
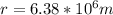
now if we plug all values in above equation
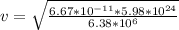
by solving above equation we have
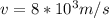
so when object is project horizontally with speed 8 km /s then it will not hit the surface but it will circulate around the earth at constant speed