The initial population was 234.
Step-by-step explanation
Formula for the exponential growth is:
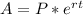 , where P is the initial amount, A is the final amount, r is the rate of growth and t is the time duration.
, where P is the initial amount, A is the final amount, r is the rate of growth and t is the time duration.
There was 337 bacteria after 5 minutes and 699 bacteria after 15 minutes. So, the equations will be......

Now dividing equation (2) by equation (1) , we will get .......
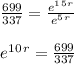
Taking 'natural log' on both sides.........
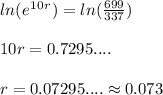
Now, plugging this
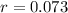 into equation (1), we will get......
into equation (1), we will get......
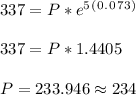
So, the initial population was 234.