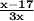Answer:
The difference of
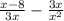 is
is
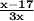
Explanation:
We need to find the difference:
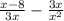
Simplifying to find the difference:
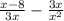
x is common in both 3x and x^2 so, we can cancel it out and we get:
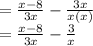
Now, taking LCM of 3x and x we get 3x, We will multiply 3x with both terms and then solve we get:
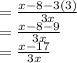
It cannot be further simplified, so we get
 as answer.
as answer.
So, The difference of
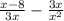 is
is