Question

Drag each equation and coordinate to the correct location on the table. Not all equations or coordinates will be used. In the table below, quadratic equations are given in standard form. Rewrite each equation in the form that reveals the maximum or minimum value, and then identify the coordinate point of that extreme value.

Answer 1

the dude above me i right i got i right on the test in edmentum

Explanation:

Answer 2

Standard Form Equivalent Form Extreme Values

y=x^2-6x+17 (x-3)^2+8 (3,8)

y=x^2+8x+21 (x+4)^2+5 (-4,5)

y=x^2-16x+60 (x-8)^2-4 (8,-4)

Explanation:

1) Standard form:

y=x^2-6x+17

Equivalent Form:

Can be found using completing the square method.

`y=x^2-6x+17\\y=x^2-2(x)(3)+(3)^2-(3)^2+17\\y=(x-3)^2-9+17\\y=(x-3)^2+8`

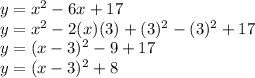
So, Equivalent form is: (x-3)^2+8

Extreme value:

Extreme values are basically the minimum and maximum value of the function.

Minimum Value will be found by finding derivative of the function:

The derivate is: 2x-6

Now, put the derivate equal to zero: 2x-6 = 0

`2x=6\\x=6/3 \\x=3`

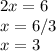
Maximum value can be found by putting minimum value in the given function:

Put x = 3 and solve:

`(3)^2-6(3)+17\\9-18+17\\9-1\\=8\\`

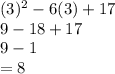
So, the extreme values is: (3,8)

2) Standard form:

y=x^2+8x+21

Equivalent Form:

Can be found using completing the square method.

`y=x^2+8x+21\\y=x^2+2(x)(4)+(4)^2-(4)^2+21\\y=(x+4)^2-16+21\\y=(x+4)^2+5`

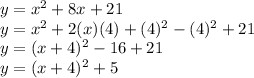
So, Equivalent form is: (x+4)^2+5

Extreme value:

Extreme values are basically the minimum and maximum value of the function.

Minimum Value will be found by finding derivative of the function:

The derivate of x^2+8x+21 is: 2x+8

Now, put the derivate equal to zero:

`2x+8 = 0\\2x=-8\\x=-8/2 \\x=-4`

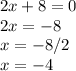
So, minimum value is: -4

Maximum value can be found by putting minimum value in the given function:

Put x = -4 and solve:

`x^2+8x+21\\=(-4)^2+8(-4)+21\\=16-32+21\\=5`

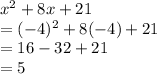
So, Maximum value is: 5

So, the extreme values is: (-4,5)

3) Standard form:

y=x^2-16x+60

Equivalent Form:

Can be found using completing the square method.

`y=x^2-16x+60\\y=x^2-2(x)(8)+(8)^2-(8)^2+60\\y=(x-8)^2-64+60\\y=(x-8)^2-4`

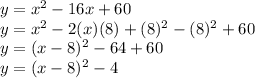
So, Equivalent form is: (x-8)^2-4

Extreme value:

Extreme values are basically the minimum and maximum value of the function.

Minimum Value will be found by finding derivative of the function:

The derivate of x^2-16x+60 is: 2x-16

Now, put the derivate equal to zero:

`2x-16 = 0\\2x=16\\x=16/2 \\x=8`

So, minimum value is: 8

Maximum value can be found by putting minimum value in the given function:

Put x = 8 and solve:

`x^2-16x+60\\=(8)^2-16(8)+60\\=64-128+60\\=-4`

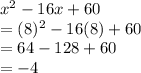
So, Maximum value is: -4

So, the extreme values is: (8,-4)