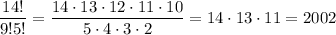Question

A mathmatics journal has accepted 14 articles for publication.however ,due to budgetary restraints only 9 articles can be published this month.how many ways can the journal editor assemble 9 of the 14 articles for publication?

Answer 1

iiiiiiiiiiiiii am not sure 69 maybe

Explanation:

Answer 2

Questions like this are answered by the binomial coefficient. The binomial coefficient
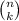`\binom{n}{k}` (read "n choose k") means exactly what you're looking for: "How many ways are there to choose k elements from a set of n elements?"

In other words, it counts the number of possible subsets of cardinality k from a set of cardinality n. It is defined as follows:

`\displaystyle \binom{n}{k} = (n!)/(k!(n-k)!)`

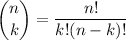
Where n! is the factorial of n:

`n! = n(n-1)(n-2)(n-3)\ldots 4 \cdot 3 \cdot 2`

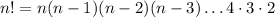
So, you have

`\displaystyle \binom{14}{9} = (14!)/(9!5!) = (14\cdot13\cdot12\cdot11\cdot10\cdot9\cdot8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2)/(9\cdot8\cdot7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot5\cdot4\cdot3\cdot2)`

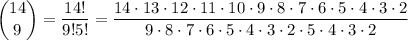
Of course, a lot of factors simplify:

`(14!)/(9!5!) = (14\cdot13\cdot12\cdot11\cdot10)/(5\cdot4\cdot3\cdot2) = 14\cdot13\cdot11 = 2002`