Question

Please Help, Thank you so much.

Answer 1

1. Writing an equation in which the quadratic expression 2x²-2x-12 equals 0.

First of all, what is a quadratic function:

The graph of a quadratic function is a special type of U-shaped curve called a parabola. In this way:

`A \ \mathbf{quadratic \ function} \ is \ given \ by:\\ \\ f(x)=ax^(2)+bx+c \\ \\ where \ a, \ b, \ and \ c \ is \ are \ real \ numbers \ with \ a\\eq 0`

So, we can write the expression above as follows:

`f(x)=2x^2-2x-12`

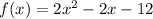
Therefore, by writing an equation making the expression equals 0, we have:

`\boxed{2x^2-2x-12=0}`

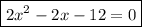
2. Showing the expression in factored form.

Factoring is the process of finding factors. This expression has the common factor of 2, so our first step is to factor out this way:

`2x^2-2x-12=0 \\ \\ \therefore 2(x^2-x-6)=0`

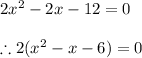
The term
`(x^2-x-6)` is a Non-perfect Square Trinomial. A Non-perfect Square Trinomial is as follows:

`(x+a)(x+b)=x^2+(a+b)x+ab`

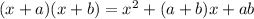
So, by using trial and error method, we need to find two numbers such that the last term is the product
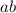`ab` and the middle term is the sum
`a+b`. These two numbers are:

`a=-3 \ and \ b=2 \\ \\ Becuase: \\ \\ a+b=-3+2=-1 \\ \\ ab=(-3)(2)=-6`

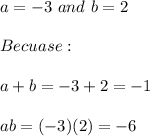
Thus, the factored form of the expression is:

`2(x-3)(x+2)=0`

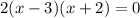
3. Explain what the solution mean for the equation

The solution for the equation are:

`x_(1)=3 \\ \\ x_(2)=-2`

These solutions are the roots of the polynomial, that is, the values at which the function
`f(x)` equals zero (x-intercepts).

Answer 2

2x² - 2x - 12 = 0

2(x² - x - 6) = 0 factored 2 on the left side

2(x - 3)(x + 2) = 0 -3 x 2 = -6 ; -3 + 2 = -1

2 = 0 , x - 3 = 0 , x + 2 = 0

false x = 3 x = -2

When the equation is graphed, the solutions are the x-intercepts.