Question

Write y=-3(x-7)^2-8 in vertex form

Answer 1

• The given equation is already in vertex form.

• The vertex is located at (7,-8)

Explanation:

We Know that a standard form of a quadratic equation is given by:

`y=ax^2+bx+c`

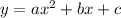
where a,b and c are real numbers

and the vertex form is given by:

`y=a(x-h)^2+k------------------(1)`

where the vertex of the function is at: (h,k)

Here we have the function as:

`y=-3(x-7)^2-8`

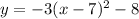
We observe that the equation matches the equation as in equation (1) ; such that a= - 3, h=7 and k= -8

Hence, the equation is already in vertex form and the vertex is at (7,-8)

Answer 2

It's in the verex form:

`f(x)+a(x-h)^2+k\\\\(h,\ k)-vertex`

`y=-3(x-7)^2-8\\\\(7,\ -8)-vertex`