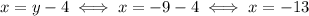Question

One number is 4 less than a second number. Twice the second number is 47 more than 5 times the first. Find the two numbers.

Answer 1

Let the two numbers be x and y, respectively the first and second. We can translate the sentences into equations:

One number is 4 less than a second number:
`x = y-4`

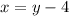
Twice the second number is 47 more than 5 times the first:
`2y = 5x+47`

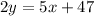
Which leads to the following linear system:

`\begin{cases} x = y-4\\2y = 5x+47\end{cases}`

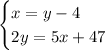
The first expression gives a way to express x in terms of y. Use this expression to substitute x in the second equation:

`2y = 5x+47 \iff 2y = 5(y-4)+47 \iff 2y = 5y -20+47 \iff -3y = 27 \iff y = -9`

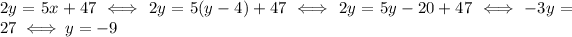
Use the first equation to deduce the value of x, now that we know the value of y:

`x = y-4 \iff x = -9-4 \iff x = -13`