Question

A set s contains 6 elements, how many different subsets can be form the elements of s that will contain exactly 4 elements

Answer 1

The binomial coefficient
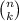`\binom{n}{k}` express exactly the number of ways you can choose k elements from a set of n elements. It is defined as

`\binom{n}{k} = (n!)/(k!(n-k)!)`

where n! express the factorial of n, which is defined as the multiplication of all number from n to 2:

`n! = n* (n-1) * (n-2) * \ldots * 3 * 2`

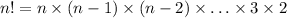
So, in your case, the number of subset of cardinality 4 that you can extract from a set of cardinality 6 is

`\binom{6}{4} = (6!)/(2!4!) = (6*5*4*3*2)/(2*4*3*2) = (6*5)/(2) = 3*5=15`