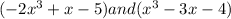
(a) To find product we multiply both expressions
First distribute -2x^3 inside the second parenthesis
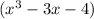
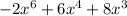
next distribute x inside the second parenthesis
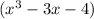
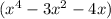
Next distribute -5 inside the second parenthesis
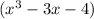
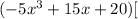
Finally we add all the product terms we got
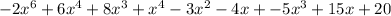
Combine like terms
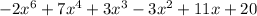
(b) yes they are same
Because interchanging of expression does not affect the product
For example 5 * 2 = 2*5 they are same.
So both the product are equal