Answer:
Option 2
Explanation:
To find : Which is an exponential growth function?
Solution :
The exponential function general form is
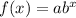
When b>1 then the function is exponentially grow.
When b<1 then the function is exponentially decay.
1)
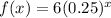
On comparing with general form, a=6 and b=0.25<1.
Function is not exponential growth function.
2)
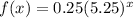
On comparing with general form, a=0.25 and b=5.25>1.
Function is an exponential growth function.
3)
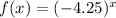
On comparing with general form, a=1 and b=-4.25<1.
Function is not exponential growth function.
4)
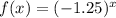
On comparing with general form, a=1 and b=-1.25<1.
Function is not exponential growth function.
Therefore, option 2 is correct.